ブログ

ケイセツの先生が普段感じたことや、皆さんにお伝えしたいことを綴っていきます。
塾生・保護者の方々はもちろん、OB･OGも気軽に参加ください。

  • HOME > 
  • ブログ
<<次の記事　前の記事>>

ふと気になった

安井校　村上 一成

皆さん、こんにちは！螢雪ゼミナール安井校・村上です。普段、校舎では英語や社会、国語を教えています。
先日、生徒が図形の問題を解いているのを見ていて、ふと気になったことがあります。
「正多角形の1つの角度って何度？」

一般的に、正ｎ角形の場合、
180 × ( n – 2 ) / n
で求まります。

これは、「多角形の内角の和」を「角の数」で割ったものになります。
だから、正三角形なら、180×(3 ｰ 2) / 3 = 60°
    正五角形なら、180×(5 ｰ 2) / 5 =108°　になります。
割りきれる数字なら、問題ありません。しかし、割り切れない数字も出てきます。例えば、正七角形、正十一角形、正十三角形、正十四角形などです。「一体、何度だろう？」「どんな形？」「そもそも今まで、出てきたことある？」何となくイメージはつきますが、気になります。気になって、夜も寝られません。(笑)
そこで、小学生のプログラミング講座で使用している「スクラッチ」というソフトを使って、小数第12位まで求めて、書いてみました。

＜正七角形＞　1つの角度は、128.571428571429°です。
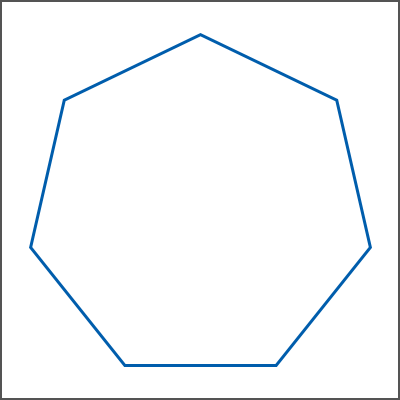
螢雪ゼミナール安井校　正七角形の角度

＜正十一角形＞　1つの角度は、147.272727272727°です。
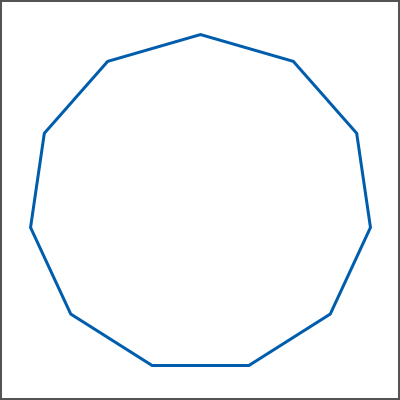
螢雪ゼミナール安井校　正11角形の角度

＜正十三角形＞　1つの角度は、152.307692307692°です。
螢雪ゼミナール安井校　正13角形の角度

＜正十四角形＞　1つの角度は、154.285714285714°です。
螢雪ゼミナール安井校　正14角形の角度

割りきれているわけではないので、「正」とつけて良いのか迷いますが、ありそうで、なさそうと思って見ておりました。(既にご存じの方がいらっしゃったら、申し訳ございません。)
いざ、手で書こうとすると難しいものでも、文明の利器に頼ると、意外と簡単に書けるので感動しました。

ふと疑問に思ったことを調べてみる、イメージしたことを具現化してみる。「まずはやってみる」というのは、おもしろいですね。それがわかると、楽しくなります。

新学期がスタートします。新しい教科書、新しい単元が始まるので、いろいろなことに興味を持つ機会が生まれます。興味を持つと勉強が楽しくなります。いろいろ勉強すると、やりたいことが見えてきます。
さあ、螢雪ゼミナール安井校で見つけよう！

なお、安井校では、新規生を受け付け中です。
【説明会お申し込み↓】
 ＷＥＢからのお申し込みはこちらから
 お電話でのお申し込みは　0120-06-4010まで

ケイセツゼミナール at 2023.3.6　11:12│comments (0)│trackback (x)│
コメント

コメントする




半角英大文字[A-Z]の4文字を入力してから送信ボタンを押してください。

最近のエントリー

最近のコメント

カテゴリー